【中２数学】連立方程式　〇％増加、△％減少の考え方

連立方程式の文章題を教えているときのこと。連立方程式を覚える以前に、「〇％増加」といった割合の考え方についての理解が不十分であると分かりました。小学校で習う概念でありますので、このタイミングで気づけてよかったです。

以下のような問題でした。

問題に記載されているとおりに、求める答えを素直にｘ、ｙとおいて解けばよい問題ですね。

長男

さて、何をｘ、ｙとおこうかな。問題文の最初に５月の合計が840kgとかいてあるから、５月のA地区をｘ、Ｂ地区をｙとおこう。

長男

えっと、次に、Ａ地区は４月に比べて10%減ったんだから、逆に考えて５月にくらべて４月が10%増えたとすればよい。同じく、Ｂ地区は15%増えたのだから５月にくらべて４月は15%減ったと考えればよいな。合計も4月から5%増えたのだから、5月の合計の5%減とすればよいから。。４月の式は、、

長男は①（５月分の式）、②（４月分の式）の連立方程式を解いて、以下のように答えを出しました。

ｘ　＝　336　、　ｙ＝５０４

きちんと整数で導出されたので、正解！と思いました。

しかし、中学生の問題にしては答えの整数値が半端な気がしました。そこで念のために答えを見てみると、やはり間違っていました。長男の計算過程を見返したところ、式の導出が間違っていることが分かりました。割合の考え方でミスがありました。

〇％増加、という割合の考え方がちょっと間違っているね。次の絵を見てみて

マルス

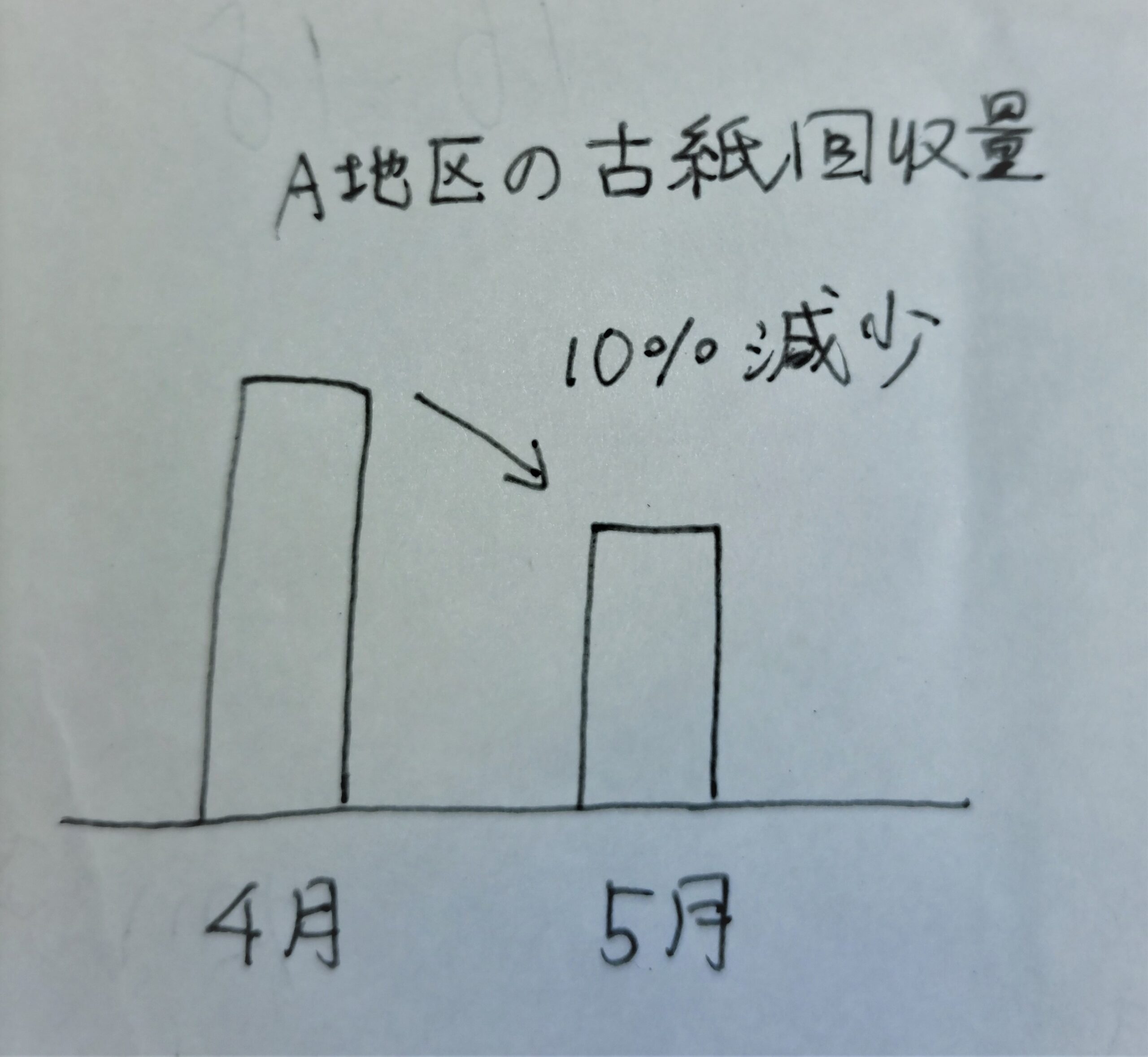
図：４月に比べて５月が１０％減少

「４月にくらべて」とあるよね。４月を仮にｚとおいてみよう。そうしたら、５月分のｘはどう表せるかな？

マルス

長男

えっと、
ｚ×０．９＝ｘ
となります

正解！すごいね
すると、４月分は
ｚ＝ｘ／０．９
と表されるよね。

マルス

長男

あ、たしかに。さきほどは、なんとなくで、
1.1ｘ　とおいてしまった。　1.1xと0.9ｘでは全く違ってくるね

そうなんだよ。よく気が付いたね。割合の問題を考えるときは、比較対象をきちんと認識することが大切です。この場合は、「４月とくらべて」とあるので、４月を基準に式を丁寧に考えよう。慣れるまでは、今回のようにもう一つの文字を使ってもいいよ

マルス

長男

うん、ｚを使うというのが分かりやすいので、この次使ってみます

ちなみに、正しい答えは、
ｘ＝３２０、ｙ＝４８０
となります。また、５月分をｘ、ｙとおくと結構大変な計算になります。正しい答えにたどり着けるとは思いますが、計算ミスを誘発するリスクがあります。こうした問題では素直に問われている内容を文字ｘ、ｙとおきましょう。

マルス

セオリー的には、素直に４月の古紙の重さをｘ、ｙとおいた方がよいですが、問題文の最初にある「５月分をあわせると８４０」にひかれて、５月をｘ、ｙとおくのもダメなことではありません。計算は大変になるため、塾や学校の教師からしたら注意を受けると思います。でも、私はユニークで面白いなと感じました。