【プログラミング】3.6 数値型

数字や数、日常では何気なく使っている言葉ですが、プログラミングの世界では一言で数と言ってもいろいろあります。そんな数の世界を見ていきましょう。

数値型

これまでに紹介したプログラムでは、数値として整数を扱ってきました。意図的に整数だけにしていたのかというと、まあそれはそうなのですが…(笑)

それはさておき、実際にプログラムで扱うことができる数値は整数には限りません。
以下に一例を示します。なお、言葉は数学の用語とはやや異なるものもあります。

表　数値の種類

整数型

これまでも扱ってきた整数です。正数、負数、0を扱うことができます。とても大きな数を扱うこともできます。

整数は、プログラム中に整数値を書くことで作ることができるほか、整数の足し算や引き算、かけ算の結果としても作ることができます。

例えば、このように作られた数はすべて整数になります。

a = 1
b = 3+4
c = 2-8
d = 12*3
e = 2**100

図　整数の例

なお、変数の型はtype()で調べることができます。例えば、以下のようにすることができます。

print(type(a))
<class 'int'>

ここで表示されるintというのが整数型を示します。intとは整数を示すintegerから来ています。

浮動小数点

小数点以下の桁を扱うことができる数です。数学における実数と似たようなものです。小数点をともなって書かれた数は、この浮動小数点数になります。

また、他の浮動小数点数による計算の結果や、整数の計算であっても割り算の結果は浮動小数点数になります。

以下の例を見てみましょう。

a = 1.5
b = 3/2
c = 2.5 + 1.5
d = 0.1*10

型を調べるとfloatになりましたね。

なお、計算結果の小数点以下が0になっても、型は整数になるわけではなく浮動小数点数のままです。浮動小数点数から整数を作りたい場合は、int()を使います。

e = 3.0
f = int(e)
print(type(e), type(f))

ところで名前の小数点数はわかりますが、「浮動」とは何なのでしょうか。
これは、浮動小数点数は内部的には「●.●●×10▲」という形式で表現されており、表現する数に応じて小数点の位置が変わりうることに起因しています。コンピュータによっては、固定小数点数が使われることもあります。

さて、コンピュータで浮動小数を扱う場合には気をつけることがあります。それは、コンピュータの浮動小数では正確な実数値を表現することができないため、計算結果が近似値で表現される可能性があることです。

例えば、以下のプログラムを見てみましょう。これは、0.001を1000回足していくものです。かけ算ではなく、足し算を繰り返しています。この場合、数学では結果は1になりますよね。ではプログラムではどうなるでしょうか？

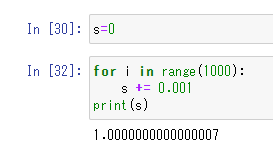
図　0.001を1000回足すと？

結果は1に近いですが、わずかに誤差のようなものが含まれています。浮動小数点数の表現の誤差が蓄積され、このような結果になってしまいました。プログラミングにおいては、このようなことにも注意が必要なのですね。

複素数

複素数とは、二乗すると-1になる虚数単位iを虚部として持つ数のことです。実部aと虚部bを組み合わせて、a+bi のような形で書き表されます。

プログラムでは、a+bjという形で記載するか、あるいはcomplex()で作ります。虚数単位の記号がiではなくjになっている点に注意です。電気の分野など、iを別の意味でよく使う分野では虚数単位としてjを使うことがあるのと同じですね。

なお、実部と虚部はそれぞれrealとimagで取り出すことができます。

a=3+2j
b=complex(2, 3)
a.real
a.imag

有理数

厳密には数値型とは少し異なるのですが、プログラムでは有理数を扱うこともできます。

有理数とは、整数の組a,bを用いてa/bの形、つまり分数の形で表現できる数のことでしたね。もちろん、bは0ではないものとします。

有理数はFraction()で作ります。有理数の機能はfractionsモジュールとして提供されるため、使う前にはimportが必要になります。

from fractions import Fraction
a=Fraction(1, 3)
b=Fraction("-2/5")
print(a+b)

分数の計算では、分母をそろえる通分が必要ですが、ちゃんと通分したうえで計算してくれています。

浮動小数点数では1/3は0.33333…となってしまいますが、有理数では1/3として扱うことができますので、正確な値を扱うことができます。

まとめ