数の性質の問題を解かせていて、公倍数の問題を解く受験テクニックよりも大切なことを教えることができました。ご紹介いたします。

期末試験が終わったので、中学校2年生に進級する前に、1年生の最初の頃に習った内容を復習させました。このような問題を出しました。
1から100までの自然数で、6の倍数、または、9の倍数である数の個数を求めなさい。
図 倍数の個数を求める問題
最初から難しい問題を出すとテンションが下がってしまいますので、ウォーミングアップをかねて易しい問題を選択してみました。すると、

図 子供の解いたノート
と書き始め、子供は次のように答えました。
答えは27個

長男
なるほど、長男は①短時間で解く受験テクニックと②集合の概念、が身についていないんだな。。

マルス
①受験テクニックの問題
まず、倍数の個数を求めるときは、このようにすべての倍数を列挙してももちろんよいですが、時間の限られる試験では非効率です。よって、次のように教えました。
6の倍数は、100÷6=16個 9の倍数は、100÷9=11個
余りは無視します。

マルス
倍数を漏れなく列挙できたのはいいね。だけどよく見てみて。たとえば、54は6の倍数でも、9の倍数でもあるから、二重に数えているよね。
長男
たしかにそうだね。


マルス
だから、この場合は、どうすればいいでしょうか
長男
6と9の最小公倍数18の個数を引けばよいから・・・100÷18=5・・・10なので、答えは27-5=22個かな


マルス
そのとおり!正解です
②集合の概念
「または」の理解が怪しいので、次の問題を出してみました。
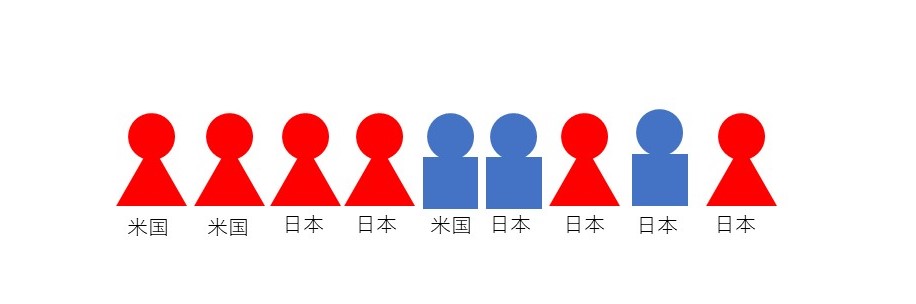
- 女性は何人いますか。
- 日本人の女性は何人いますか。
- 米国人の女性、または、日本人の女性は何人いますか。
- 日本人で、かつ、女性である人は何人いますか。
図 米国人の男女と日本人の男女の人数を数える問題
1と2は当然答えました。そして、問題3について、
米国人の女性が2人、日本人の女性が3人

長男
ここで原因が分かりました。「または」を理解していなかったのです。

マルス
この問題は、1と同じ答えなんだよ。「または」は「どちらかが正しければOK」といった意味なので、「米国人の女性」という条件と、「日本人の女性」という条件のどちらかを満たしていれば人数に数えていいんだよ
なるほど!理解しました。ありがとう

長男

マルス
次に、「かつ」です。これはAかつB、のとき、AとBの条件を両方満たすことが必要という意味になります。この考え方で問題4を考えてみるとどうなるかな
えっと、この場合は、日本人であり、同時に女性であることが必要だから・・・、1,2,3。3人だね

長男

マルス
はい、正解!この「または」と「かつ」はプログラミングで重要な概念になります。ちなみに、それぞれ、「or」、「and」と書きます。覚えておくといいよ♪
まとめ
- 「または」と「かつ」の意味は、ここで正確に覚えてしまおう
- 「または」は「どちらかが正しければOK」といった意味
- 「かつ」は両方が正しいことが必要。AかつB、のとき、AとBの条件を両方満たすことが必要という意味になります。



コメント